2018年沪教版三年级数学下册《谁围出的面积最大》教案设计(2)
反馈学生的记录表,通过投影仪展示,让学生体会有序思考有序排列的优点,可以不重复、不遗漏找到所有的可能。
2. 观察记录下的表格,讨论以下问题:
(1)20根小棒一共可以围成几种不同形状的长方形?
(2)这些长方形的周长都是20,为什么?
(3)周长是20,怎样确定长方形的长和宽呢? 周长的一半就是一个长加宽的和。
(4)这些长方形的周长相等,它们的面积相等吗?面积为什么不相等呢? 这些长方形的周长相等,围成的长方形的长和宽各不相等,所以围成的长方形的面积不相等。
(5)长方形的长和宽的长度和它的面积大小之间有什么关系? 这些周长相等的长方形中, 长方形的长和宽的长度相差越大,面积就越小。 长方形的长和宽的长度相差越小,面积就越大。 当围成的长方形长与宽相等成为正方形时,面积最大。 你还能从这些记录中发现什么? 小结并板书 :长方形周长一定时,长方形长与宽越接近,它的面积就越大;反之,长方形长与宽相差越大,它的面积就越小,当长与宽相等时,即正方形面积最大。
(二)验证规律
师:如果小棒的根数不是20根,是否也有这样的规律呢?小组认领任务:14根、16根、22根。
1. 能不能不用摆小棒,围出所有的长方形,完成表格(二)。
根小棒围出长方形
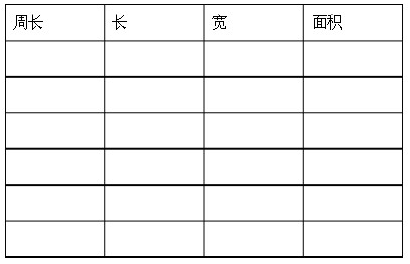
2. 学生汇报。
小结:知道周长,要围出长方形,先确定它的长和宽; 当周长一定时,长与宽越接近,面积越大;长与宽相差越大,面积越小。 今天我们探究的就是“谁围出的面积最大”(板书)
三、实践运用
1. 回到小欧拉的故事,现在你知道小欧拉是怎样改羊圈的吗?你知道围最大的面积在生活中有什么用处吗?
2. 养蟹场要新建一个长方形蟹塘,为防止蟹逃走,四周需要用网围起来。网的长度是80米,怎样围,蟹塘的面积最大?
3. 围最大的面积不仅可以解决很多生活中的问题,还可以解决很多数学问题。比一比,谁做得又对又快: 两个自然数的和是60,你认为这两个自然数的积最大是( ); 两个自然数的和是41,你认为这两个自然数的积最大是( )。


 小学家长最新升学资料下载
小学家长最新升学资料下载





